• 学習・教育

別世界の住人のように思える「推し」も、知り合いの知り合いをたどれば、意外と身近なところでつながっているかもしれません。

子どもから大人まで楽しめる数の雑学を、『すごすぎる数の図鑑』よりご紹介します。

※本記事は渡邉究著『すごすぎる数の図鑑』(KADOKAWA)より一部抜粋、編集したものです。

「6次の隔たり」で推しともつながれる! ?

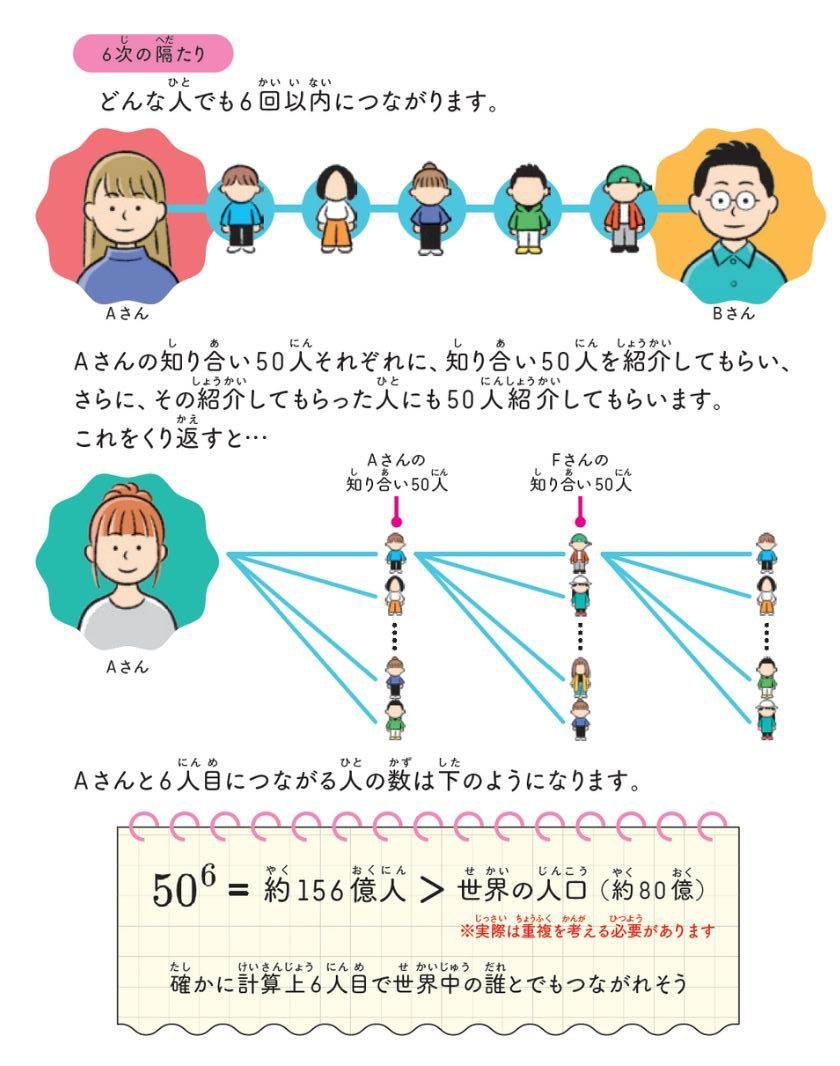
世界中のどんな人でも、知り合いをたどれば、6人以内でつながることができるという仮説を「6次の隔たり」といいます。

たとえば、あなたの友達の友達の……と続けていくと、6回以内で世界中の誰とでもつながることができるということです。

この仮説は、1967年にアメリカの心理学者スタンレー・ミルグラムが行った「スモールワールド実験」で検証されました。

彼は、アメリカのある地域に住む住民に手紙を渡し、直接知らない相手に届けるために、知り合いを通じて手紙を送るよう依頼しました。

結果として、平均して5人を介して手紙が目的の人に届いたのです。

この「6次の隔たり」は、SNSが普及した現代では、さらに距離が縮まっていると考えられています。

たとえば、あるSNSの調査では、平均して4人を介せばそのSNSのどんなユーザーともつながることができると報告されています。

もしかしたらあなたの友達をたどると、どこかで「推し」とつながるかもしれません。

いつか「推し」ともつながれる？

「6次の隔たり」を計算を用いて考えてみましょう。